Java递归函数Recursive算法讲解系列五

递归的缺点和问题

虽然递归是一种非常强大的工具，但它很容易被以各种方式滥用。在本节中，我们将研究几个实施不当的重新诅咒会导致严重的效率低下的情况，并讨论一些识别和避免此类陷阱的策略。

我们首先回顾上一章文章中定义的元素唯一性问题。我们可以使用下面的递归公式来确定序列的n个元素是否都是唯一的。作为基本情况，当n=1时，元素通常是唯一的。对于n≥2，当且仅当前n−1个元素是唯一的，最后n−1个元素是唯一的，并且第一个和最后一个元素是不同的（因为这是唯一一个没有被检查为子类的对）。基于此思想的递归实现在代码片段中给出，名为unique3（以区别于上一章中的unique1和unique2）。

/∗∗ Returns true if there are no duplicate values from data[low] through data[high].∗/
 public static boolean unique3(int[ ] data, int low, int high) {
	 if (low >= high) 
	 	return true; // at most one item
	 else if (!unique3(data, low, high−1)) 
	 	return false; // duplicate in first n−1
	 else if (!unique3(data, low+1, high)) 
	 	return false; // duplicate in last n−1
	 else 
	 	return (data[low] != data[high]); // do first and last differ?
 }

不幸的是，这是一个非常低效的递归使用。每个调用的非递归部分使用O（1）时间，因此总的运行时间将与递归调用的总数成比例。为了分析这个问题，我们让n表示考虑中的条目数，也就是说，让n=1+high-low。

如果n=1，那么unique3的运行时间是O（1），因为这种情况下没有递归调用。在一般情况下，重要的观察是，对大小为n的问题的unique3的单个调用可能导致对大小为n−1的问题进行两次递归调用。这两个大小为n−1的调用反过来可能会导致四个大小为n−2的调用（每个调用两个），从而导致8个大小为n−3的调用，依此类推。因此，在最坏的情况下，方法调用的总数由几何求和给出

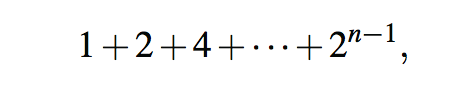
根据命题等于2n−1。因此，方法unique3的运行时间是O（2n）。对于解决元素唯一性问题来说，这是一种极其低效的方法。它的低效并不是因为它使用递归，而是因为它使用递归很差。

计算Fibonacci数的一种低效递归算法

我们介绍了一个生成Fi-bonacci数级数的过程，该过程可递归定义如下：

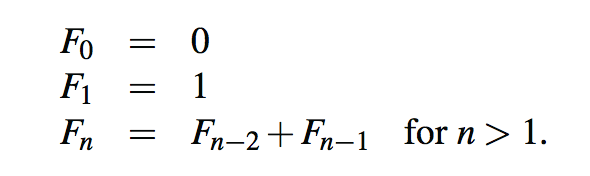
讽刺的是，直接基于这个定义的递归实现会产生代码片段中所示的fibonacciBad方法，该方法通过在每个非基本情况下进行两次递归调用来计算一个Fibonacci数。

/∗∗ Returns the nth Fibonacci number (inefficiently). ∗/
 public static long fibonacciBad(int n) {
	 if (n <= 1)
	 	return n;
	 else
	 	return fibonacciBad(n−2) + fibonacciBad(n−1);
 }

不幸的是，这种直接实现Fibonacci公式的结果是一个非常低效的方法。以这种方式计算第n个Fibonacci数需要对方法进行指数级调用。具体地说，让cn表示在执行fibonacciBad（n）时执行的调用数。然后，我们得到cn的以下值：

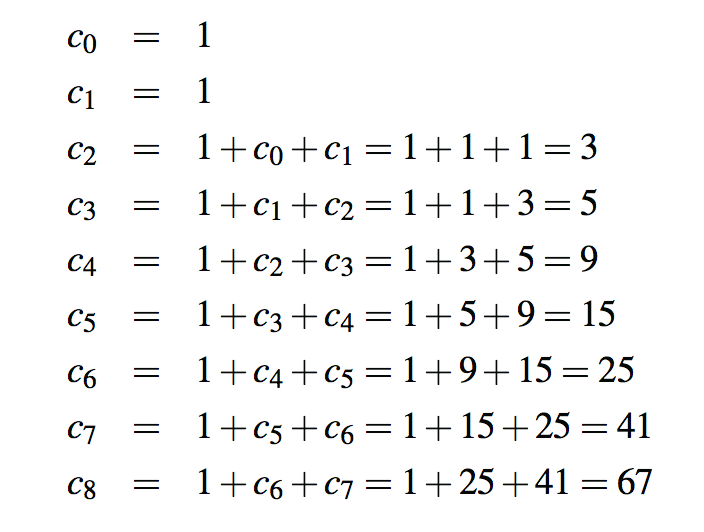
如果我们按照这个模式前进，我们会发现，每两个连续的索引，调用的数量都会增加一倍以上。也就是说，c4是c2的两倍以上，c5是c3的两倍以上，c6是c4的两倍以上，依此类推。因此，cn>2n/2，这意味着fibonacciBad（n）发出的调用数在n中是指数级的。

计算Fibonacci数的一种有效递归方法

因为第n个Fibonacci数Fn依赖于前面两个值Fn−2和Fn−1，我们被诱惑使用了糟糕的递归公式。但是请注意，在计算Fn−2之后，对compute Fn−1的调用需要自己的递归调用来计算Fn−2，因为它不知道在早期递归级别计算的Fn−2的值。那是重复劳动。更糟糕的是，这两个调用都需要（重新）计算Fn−3的值，以及Fn−1的计算。正是这种滚雪球效应导致了腓肠肌的指数运行时间。

我们可以更有效地使用递归计算Fn，其中每个调用只进行一个递归调用。为此，我们需要重新定义方法的经验。我们没有让方法返回一个值，即第n个Fibonacci数，而是定义了一个递归方法，该方法使用F−1=0的约定，返回具有两个连续Fibonacci数{Fn，Fn−1}的数组。虽然报告两个连续的Fibonacci数而不是一个似乎是一个更大的负担，但是将这些额外的信息从一个递归级别传递到下一个级别，使得继续该过程更加容易。（它允许我们避免重新计算递归中已知的第二个值。）基于此策略的实现在代码片段5.14中给出。

/∗∗ Returns array containing the pair of Fibonacci numbers, F(n) and F(n−1). ∗/
 public static long[ ] fibonacciGood(int n) {
	 if (n <= 1) {
	 	long[ ] answer = {n, 0};
	 	return answer;
	 } else {
		 long[ ] temp = fibonacciGood(n − 1); // returns {Fn−1, Fn−2}
		 long[ ] answer = {temp[0] + temp[1], temp[0]}; // we want {Fn, Fn−1}
		 return answer;
	 }
 }

就效率而言，对于这个问题，坏的和好的递归之间的区别就像白天和黑夜一样。fibonacciBad方法使用指数时间。我们声称fibonacciGood（n）方法的执行在O（n）时间内运行。每次对fibonacciGood的递归调用都会将参数n减少1；因此，递归跟踪包括一系列n个方法调用。因为每个调用的非递归工作使用恒定时间，所以整个计算在O（n）时间内执行

Java中的最大递归深度

滥用递归的另一个危险是无限递归。如果每个递归调用都执行另一个递归调用，而没有达到基本情况，那么我们就有一个无限系列的此类调用。这是一个致命的错误。无限递归可以迅速地淹没计算资源，这不仅是由于CPU的快速使用，而且因为每个连续的调用都会创建一个需要额外内存的帧。下面是格式错误的递归的一个明显例子：

/∗∗ Don't call this (infinite) version. ∗/
public static int fibonacci(int n) {
    return fibonacci(n); // After all Fn does equal Fn
}

然而，还有更细微的错误会导致无限递归。重温我们的二进制搜索实现，当我们对序列的右侧部分进行递归调用时，我们指定从索引mid+1到high的子数组。那句话是不是改成了

return binarySearch(data, target, mid, high); // sending mid, not mid+1

这可能导致无限递归。特别是，当搜索两个元素的范围时，可以对相同的范围进行递归调用。

程序员应该确保每个递归调用都在某种程度上朝着一个基本情况前进（例如，通过使参数值随每次调用而减少）。为了对抗无限递归，Java的设计者有意地决定限制用于存储同时活动方法调用的激活帧的总空间。如果达到此限制，Java虚拟机将抛出StackOverflowError。此限制的精确值取决于Java安装，但一个典型值可能允许1000个以上的同时调用。

对于许多递归应用程序，允许多达1000个嵌套调用就足够了。例如，我们的二进制搜索方法具有O（logn）递归深度，因此要达到默认的递归限制，需要21000个元素（远远超过宇宙中估计的原子数）。然而，我们已经看到了一些递归深度与n.Java对递归深度的限制成比例的线性递归可能会破坏这种计算。

可以重新配置Java虚拟机，以便为嵌套方法调用提供更大的空间。这是通过在启动Java时设置-Xss runtime选项来实现的，可以作为命令行选项，也可以通过IDE的设置来实现。但通常可以依赖递归算法的直觉，而不是使用方法调用来表示必要的重复，而是更直接地重新实现它。我们只讨论这样一种方法来结束这一章。

消除尾递归

递归算法设计方法的主要优点是，它允许我们简洁地利用许多问题中存在的重复结构。通过使我们的算法描述以递归的方式利用重复结构，我们通常可以避免复杂的案例分析和嵌套循环。这种方法可以导致更具可读性的算法描述，同时仍然相当有效。

然而，递归的有用性是以适度的代价来实现的。特别是，Java虚拟机必须维护跟踪每个嵌套调用状态的帧。当计算机内存处于高级状态时，派生递归算法的非递归实现是有益的。

一般来说，我们可以使用堆栈数据结构，通过人工调整递归结构的嵌套，而不是依赖解释器来将递归算法转换为非递归算法。虽然这只会将内存使用从预处理程序转移到堆栈，但我们可以通过存储所需的最小信息来进一步减少内存使用量。

更妙的是，某些形式的递归可以在不使用辅助内存的情况下被消除。其中一种形式被称为尾部递归。如果从一个上下文中进行的任何递归调用是该上下文中的最后一个操作，则递归就是尾部递归，递归调用的返回值（如果有）由封闭递归立即返回。根据需要，尾部递归必须是线性递归（因为如果必须立即返回第一个递归调用的结果，则无法进行第二个递归调用）。

在本章演示的递归方法中，代码片段的二进制搜索方法和代码片段的reverseArray方法都是尾部递归的示例。我们的其他一些线性递归几乎类似于尾部递归，但技术上不是这样。例如，代码片段的阶乘方法不是尾部递归。最后是命令：

return n ∗ factorial(n−1);

这不是尾部递归，因为在递归调用完成后执行了一个额外的乘法运算，返回的结果不一样。出于类似的原因，代码片段的linearSum方法、代码示例中的幂方法以及fibonacciGood方法都不能作为尾部递归。

尾部递归是特殊的，因为它们可以通过将主体封闭在循环中以进行重复，并通过将现有参数重新分配给这些值来用新参数替换递归调用，从而自动地非递归地重新实现。事实上，许多编程语言实现可以用这种方式转换尾部递归作为一种优化。

/∗∗ Returns true if the target value is found in the data array. ∗/
 public static boolean binarySearchIterative(int[ ] data, int target) {
	 int low = 0;
	 int high = data.length − 1;
	 while (low <= high) {
		 int mid = (low + high) / 2;
		 if (target == data[mid]) // found a match
		 	return true;
		 else if (target < data[mid])
		 	high = mid − 1; // only consider values left of mid
		 else
	 		low = mid + 1; // only consider values right of mid
	 }
	 return false; // loop ended without success
 }

作为一个具体的例子，我们的binarySearch方法可以重新实现，如代码示例所示。我们在while循环之前初始化变量low和high来表示数组的完整范围。然后，在循环的每个过程中，我们要么找到目标，要么缩小候选子射线的范围。在原始版本中进行递归调用binarySearch（data，target，low，mid−1），我们只需在新版本中替换high=mid−1，然后继续循环的下一个迭代。我们最初的基本情况条件low>high已被相反的循环条件所取代，而low<=high。在我们的新实现中，如果while循环结束时从未从内部返回true，则返回false以指定失败的搜索。

大多数其他的线性递归可以通过迭代非常有效地表达，即使它们不是形式上的尾部递归。例如，对于计算阶乘、计算斐波纳契数、求和数组元素或反转数组的内容，有一些简单的非递归实现。例如，代码示例提供了一个非递归方法来反转数组的内容（与下面代码的递归方法相比）。

/∗∗ Reverses the contents of the given array. ∗/
 public static void reverseIterative(int[ ] data) {
	 int low = 0, high = data.length − 1;
	 while (low < high) { // swap data[low] and data[high]
		 int temp = data[low];
		 data[low++] = data[high]; // post-increment of low
		 data[high−−] = temp; // post-decrement of high
	 }
 }