Java递归函数recursive算法讲解系列四

用递归反转序列

让我们考虑一个数组的n个元素的倒序问题，以便第一个元素成为最后一个元素，第二个元素成为倒数第二个元素，依此类推。我们可以使用线性递归来解决这个问题，通过观察序列的反转可以通过交换第一个和最后一个元素，然后递归地反转剩余的元素来实现。我们在代码中给出了该算法的一个实现，使用的约定是，我们第一次将此算法称为reverseArray（data，0，n−1）。

/∗∗ Reverses the contents of subarray data[low] through data[high] inclusive. ∗/
 public static void reverseArray(int[ ] data, int low, int high) {
	 if (low < high) { // if at least two elements in subarray
		 int temp = data[low]; // swap data[low] and data[high]
		 data[low] = data[high];
		 data[high] = temp;
		 reverseArray(data, low + 1, high − 1); // recur on the rest
	 }
 }

我们注意到，每当进行递归调用时，数组相关部分中的元素将减少两个。当条件low<high失败时，最终达到一个基本情况，原因是n为奇数时low==high，或n为偶数时low==high+1。

上面的参数意味着代码中的递归算法保证在总共1+n次递归调用之后终止。每次打电话都是因为如果子阵列中至少有两个元素交换数据[low]和data[high]，涉及一个恒定的工作量，整个过程在O（n）时间内运行。

计算幂的递归算法

作为使用线性递归的另一个有趣的例子，我们考虑将一个数x提升为任意非负整数n的问题。也就是说，我们希望计算幂函数，定义为幂（x，n）=xn。（我们在讨论中使用“power”这个名称，以区别于Math类的pow方法，后者提供了这样的功能。）我们将考虑两种不同的递归公式来解决导致算法性能截然不同的问题。

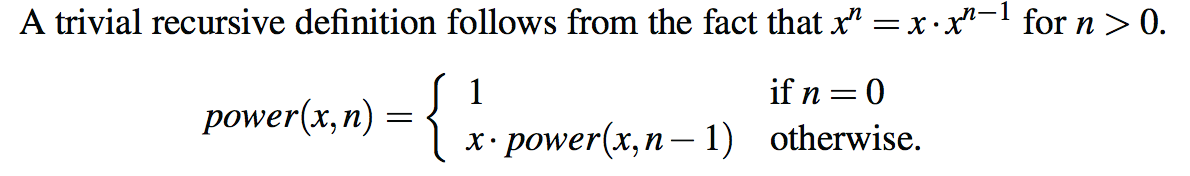
/∗∗ Computes the value of x raised to the nth power, for nonnegative integer n. ∗/
 public static double power(double x, int n) {
	 if (n == 0)
	 	return 1;
	 else
	 	return x ∗ power(x, n−1);
 }

对这个power（x，n）版本的递归调用在O（n）时间内运行。它的递归跟踪结构与图中的阶乘函数的结构非常相似，每次调用时参数都会减少一个，并且在n+1级别的每个级别上都执行恒定的工作。

然而，有一种更快速的方法来计算幂函数，使用另一种定义，即使用平方技术。设k=n表示整数除法的底数（当n是int时，相当于Java中的n/2）。我们考虑如下方式：

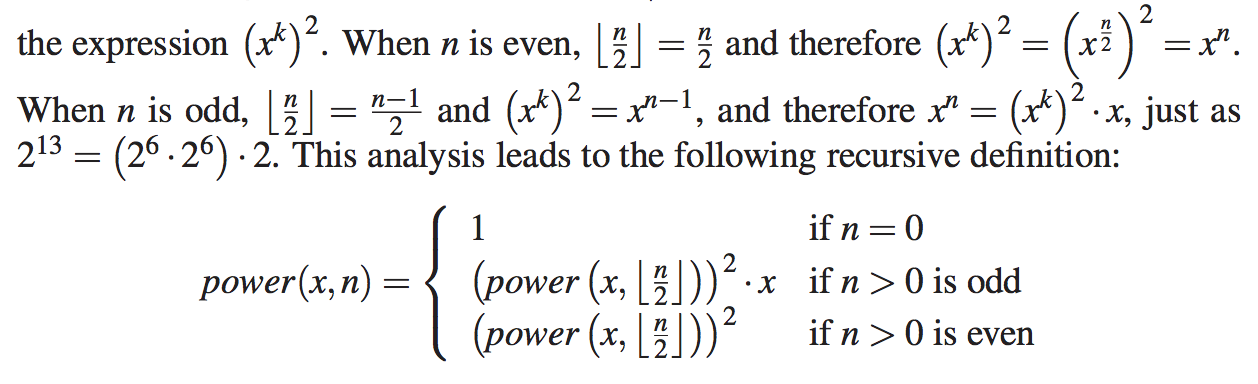
/∗∗ Computes the value of x raised to the nth power, for nonnegative integer n. ∗/
 public static double power(double x, int n) {
	 if (n == 0)
	 	return 1;
	 else {
		 double partial = power(x, n/2); // rely on truncated division of n
		 double result = partial ∗ partial;
	 if (n % 2 == 1) // if n odd, include extra factor of x
		 result ∗= x;
		 return result;
	 }
 }

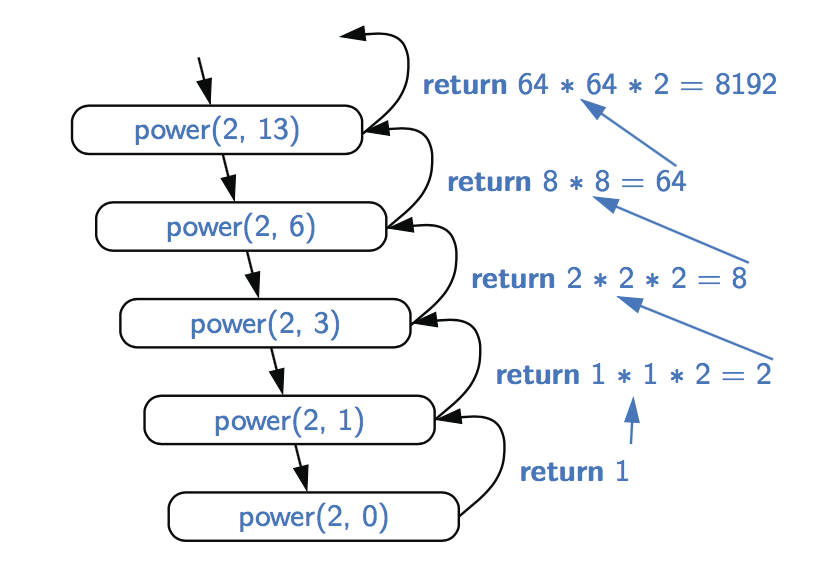
为了说明改进算法的执行，图中提供了一个计算能力的递归跟踪power(2, 13)。

为了分析修正算法的运行时间，我们观察到每次方法幂（x，n）的递归调用中的元素最多为前一个指数的一半。正如我们在二进制搜索的分析中看到的，在得到1或更少之前，我们可以将n除以2的次数是O（logn）。因此，我们新的幂函数公式会导致O（logn）递归调用。方法的每个单独激活都使用O（1）操作（不包括递归调用），因此计算power（x，n）的操作总数为O（logn）。这是对原O（n）时间算法的一个显著改进。

改进后的版本在减少内存使用方面也提供了显著的节省。第一个版本的递归深度为O（n），因此O（n）帧同时存储在内存中。因为改进版本的递归深度是O（logn），所以它的内存使用量也是O（logn）。

二进制递归

当一个方法进行两次递归调用时，我们说它使用二进制递归。我们已经看到了绘制英制标尺时二进制递归的例子（上一篇递归示例）。作为二进制递归的另一个应用，让我们重新讨论一下数组的n个整数求和的问题。计算一个或零值之和是微不足道的。对于两个或两个以上的值，我们可以递归地计算前半部分的和和和后一半的和，并将这些和相加。在代码中，我们对这种算法的实现最初被调用为binarySum（data，0，n−1）。

/∗∗ Returns the sum of subarray data[low] through data[high] inclusive. ∗/
 public static int binarySum(int[ ] data, int low, int high) {
	 if (low > high) // zero elements in subarray
	 	return 0;
	 else if (low == high) // one element in subarray
	 	return data[low];
	 else {
		 int mid = (low + high) / 2;
		 return binarySum(data, low, mid) + binarySum(data, mid+1, high);
	 }
 }

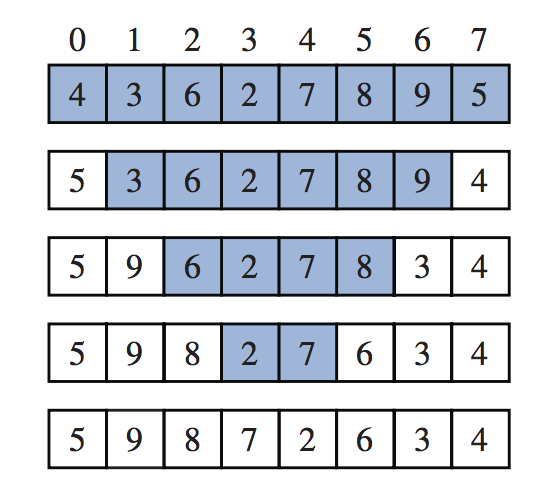
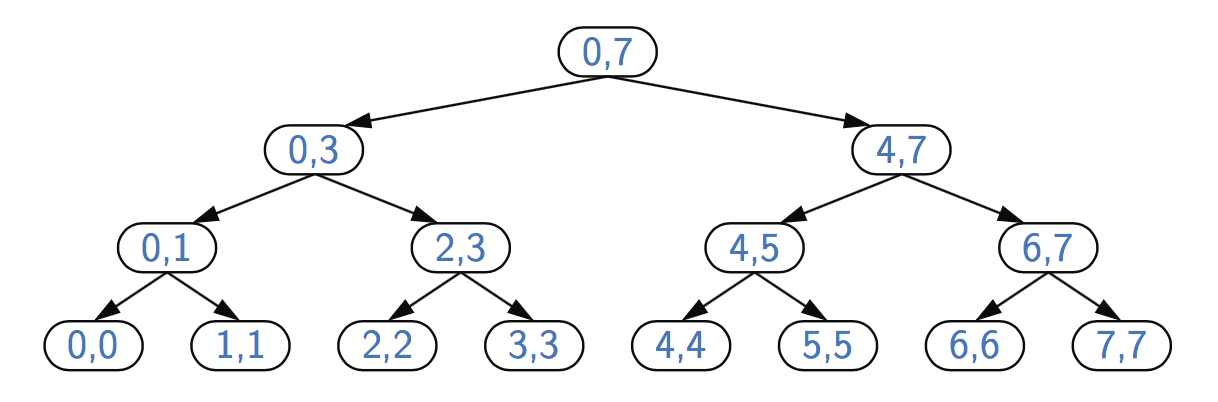
为了分析二进制求和算法，为了简单起见，我们考虑了n是2的幂的情况。图5.13显示了binarySum（data，0，7）执行的递归跟踪。我们用该调用的参数值low和high标记每个框。在每次递归调用时，范围的大小被一分为二，因此递归的深度是1+log2n。因此，binarySum使用O（logn）的额外空间，这比代码中linearSum方法使用的O（n）空间有很大的改进。但是，binarySum的运行时间是O（n），因为有2n−1个方法调用，每个调用都需要固定的时间。

多重递归

从二进制递归中推广，我们将多重递归定义为一个过程，其中一个方法可以进行两个以上的递归调用。我们分析文件系统磁盘空间使用情况的递归是多重递归的一个例子，因为在一次调用期间进行的递归调用的数量等于文件系统给定目录中的条目数。

多重递归的另一个常见应用是当我们想要枚举各种配置以解决组合难题时。例如，以下是所有被称为求和谜题的实例：

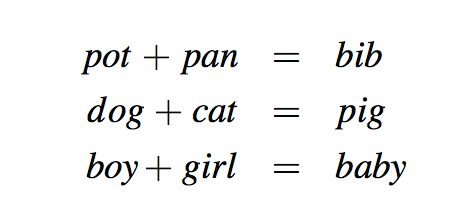
为了解决这个难题，我们需要给等式中的每个字母指定一个唯一的数字（即0，1，…，9），以使方程成立。通常，我们通过对我们试图解决的特定难题的人类观察来解决这样一个难题，以消除配置（即，可能的数字到字母的部分分配），直到我们能够处理剩余的可行配置，测试每个配置的正确性。

然而，如果可能配置的数量不是太多，我们可以使用计算机简单地列举所有的可能性并测试每一种可能性，而不需要人工观察。这种算法可以使用多重递归来系统地处理配置。为了保持描述的通用性，以便与其他谜题一起使用，我们考虑了一种算法，该算法从给定的宇宙U中选择并测试所有k长度的序列，无需重复。我们在代码中展示了这种算法的伪代码，通过以下步骤构建k个元素的序列：

1. 递归生成k−1元素序列
2. 在每个这样的序列中附加一个尚未包含在其中的元素

在整个算法的执行过程中，我们使用一个集合U来跟踪当前序列中没有包含的元素，因此当且仅当e是inU时，元素e还没有被使用。

另一种看待代码片段算法的方法是，它枚举U的每一个可能的大小为k的有序子集，并测试每个子集是否是我们难题的可能解决方案。

对于求和谜题，U={0，1，2，3，4，5，6，7，8，9}并且序列中的每个位置对应于一个给定的字母。例如，第一个位置可以代表b，第二个代表o，第三个代表y，依此类推。

Algorithm PuzzleSolve(k, S, U):
	Input: An integer k, sequence S, and set U
	Output: An enumeration of all k-length extensions to S using elements in U
		without repetitions
	for each e in U do
		Add e to the end of S
		Remove e from U {e is now being used}
		if k = = 1 then
			Test whether S is a configuration that solves the puzzle
			if S solves the puzzle then
				add S to output {a solution}
		else
			PuzzleSolve(k−1, S, U) {a recursive call}
		Remove e from the end of S
		Add e back to U

在图中，我们展示了对PuzzleSolve（3，S，U）调用的递归跟踪，其中S为空，U={a，b，c}。在执行过程中，生成并测试三个字符的所有排列。最初的三个调用依次进行两个递归调用。如果我们在一个由四个元素组成的集合U上执行PuzzleSolve（3，S，U），初始调用将进行四次递归调用，每个调用都有一个如图所示的轨迹。

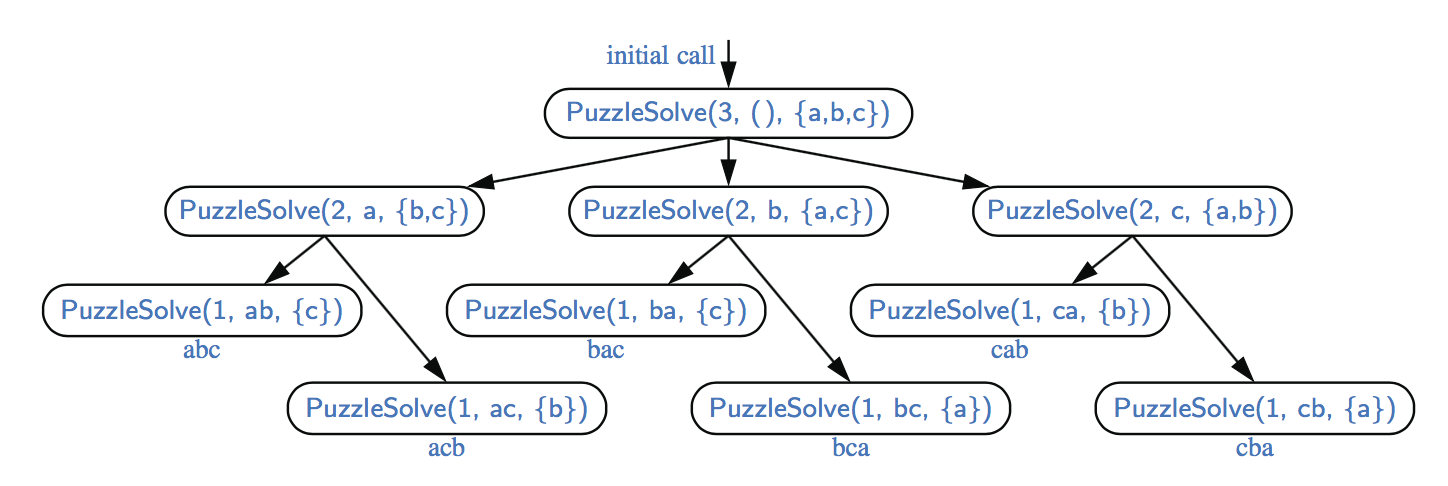
执行PuzzleSolve（3，S，U）的递归跟踪，其中S为空，U={a，b，c}。此执行生成并测试a、b和c的所有置换。我们将在它们各自的框的正下方显示生成的置换。

使用递归的算法通常具有以下形式：

• 基本情况测试。我们首先测试一组基本情况（至少应该有一个）。应该定义这些基本用例，以便每个可能的递归调用链最终都会到达一个基本用例，并且每个基本用例的处理不应该使用递归。
• 复发。如果不是基本情况，则执行一个或多个递归调用。此重复步骤可能涉及一个测试，该测试决定要进行几个可能的递归调用中的哪一个。我们应该定义每个可能的递归调用，以便它朝着一个基本情况前进。

参数化递归

为了设计一个给定问题的递归算法，我们可以考虑不同的方法来定义与原始问题具有相同总体结构的子问题。如果一个人很难找到设计递归算法所需的重复结构，那么有时可以通过几个具体的例子来解决问题，看看如何定义子问题。

成功的递归设计有时需要我们重新定义原始问题，以便于类似的子问题。通常，这涉及重新参数化方法的签名。例如，在数组中执行双线性搜索时，调用者的自然方法签名将显示为binarySearch（data，target）。然而，我们定义了我们的方法，调用签名二进制搜索（data，target，low，high），在递归过程中使用附加参数来划分子数组。参数化的这种变化对于二进制搜索是至关重要的。本章中的其他几个示例（例如reverseArray、linearSum、binarySum）也演示了在定义递归子问题时使用附加参数。

如果我们希望为算法提供一个更干净的公共接口，而不向用户公开递归参数化，标准技术是使递归版本私有化，并引入一个更干净的公共方法（用适当的参数调用私有方法）。例如，我们可以提供以下更简单的binarySearch版本供公众使用：

/∗∗ Returns true if the target value is found in the data array. ∗/
public static boolean binarySearch(int[ ] data, int target) {
	return binarySearch(data, target, 0, data.length − 1); // use parameterized version
}

这个递归视频演示了递归算法的过程：