Java递归函数与算法讲解系列三

递归跟踪

为了产生不同形式的递归跟踪，我们在Java实现中包含了一个无关的print语句。该输出的精确格式有意地镜像了一个名为du的经典Unix/Linux实用程序（用于“disk usage 磁盘使用”）生成的输出。它报告一个目录所使用的磁盘空间量和嵌套在其中的所有内容，并可以生成一个详细的报告。

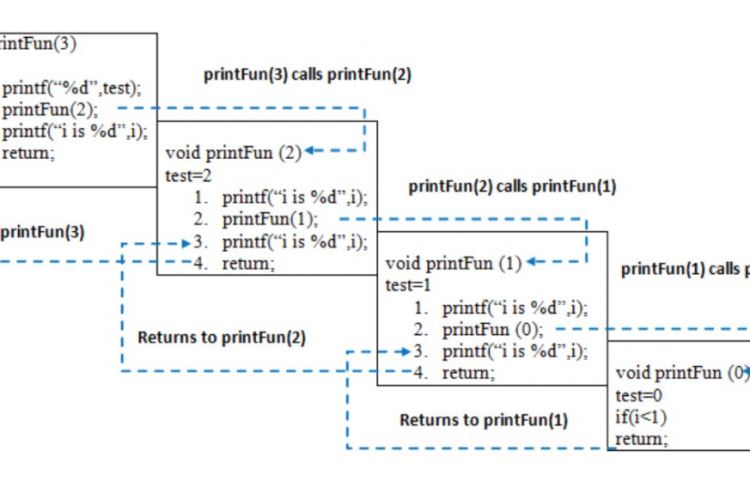
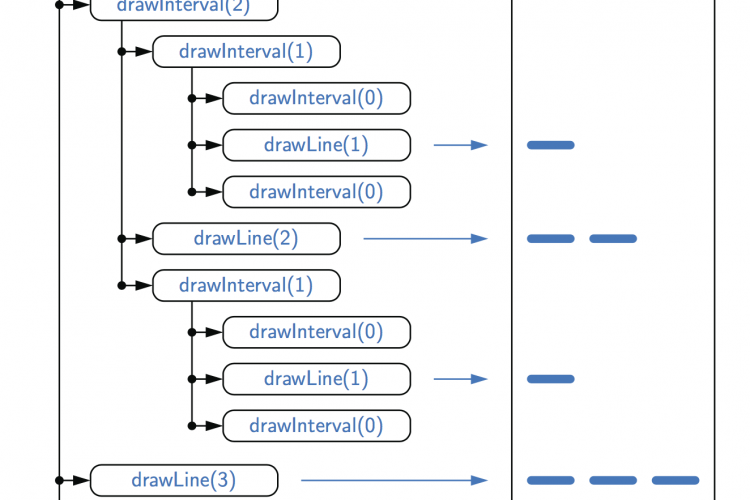
当在示例文件系统上执行时，我们对diskUsage方法的实现会产生下图给出的结果。在算法的执行过程中，对所考虑的文件系统部分中的每个条目只进行一次递归调用。因为每一行都是在递归调用返回之前打印的，所以输出行反映了递归调用完成的顺序。请注意，它先计算并报告嵌套项的累积磁盘空间，然后再计算和报告包含该项的目录的累积磁盘空间。例如，在计算包含它们的目录/user/rt/courses/cs016的累计总数之前，计算与条目成绩、家庭作业和程序有关的递归调用。

分析递归算法

在上一篇文章中我们介绍了分析一个算法效率的数学技术，基于对算法执行的原始操作数量的估计。我们用大数和大数之间的关系来概括。在本节中，我们将演示如何对递归算法执行这种类型的运行时分析。

使用递归算法，我们将根据在执行时管理控制流的方法的特定激活来说明执行的每个操作。换句话说，对于方法的每次调用，我们只考虑在激活主体中执行的操作的数量。然后，我们可以计算作为递归算法一部分执行的操作的总数量，方法是在所有激活中计算每次激活期间发生的操作数的总和。（顺便说一句，这也是我们分析一个非递归方法的方法，该方法从其主体中调用其他方法。）

为了证明这种分析方式，我们重新讨论了上节中提出的四种递归算法：阶乘计算、绘制英语标尺、二进制搜索和文件系统累积大小的计算。一般来说，我们可以依靠递归跟踪所提供的直觉来识别发生了多少次递归激活，以及如何使用每个激活的参数化来估计在该激活体中发生的原始操作的数量。然而，每种递归算法都有其独特的结构和形式。

计算阶乘

如上节所述，分析我们计算阶乘的方法的效率相对容易。为了计算阶乘（n），我们看到总共有n+1次激活，因为参数从第一次调用中的n减少到第二次调用中的n−1，依此类推，直到到达参数为0的基本情况。

通过对代码片段中的方法体的检查，还可以清楚地看到，factorial的每个单独激活都执行一个恒定数量的操作。因此，我们得出结论，计算阶乘（n）的操作总数是O（n），因为有n+1个激活，每个激活都占O（1）操作。

画英国尺子

在分析英制标尺应用程序时，我们考虑了一个有趣的问题，即最初调用drawInterval（c）生成了多少行输出，其中c表示中心长度。这是算法整体效率的一个合理的基准点，因为每一行输出都基于对drawLine实用程序的调用，而对drawInterval的每次递归调用都只对drawLine进行一次直接调用。

通过检查源代码和重现跟踪可以获得一些直觉。我们知道，对c>0的drawInterval（c）的调用会产生两个对drawInterval（c−1）的调用和对drawLine的单个调用。我们将依靠这个直觉来证明下面的说法。

命题：对于c≥0，调用drawInterval（c）将精确地生成2c−1行输出。

理由：我们通过归纳提供了这一索赔的正式证明。事实上，归纳法是证明递归过程正确性和效率的自然数学方法。对于标尺，我们注意到drawInterval（0）应用程序不会生成输出，而20−1=1−1=0。这是我们索赔的基本依据。

更一般地说，drawInterval（c）打印的行数是调用drawInterval（c−1）生成的行数的两倍多，因为两个递归调用之间打印一条中心线。通过归纳，我们得到线的数量因此为1+2·（2c−1−1）=1+2c−2=2c−1。

这一证明表明了一种更严格的数学工具，即递归方程，可用于分析递归算法的运行时间。在递归排序算法的上下文中讨论了该技术。

执行二进制搜索

考虑到在二进制搜索过程中每一次执行的二进制运算次数都为1.5。因此，运行时间与执行的递归调用的数量成正比。我们将证明，在对包含n个元素的序列进行二进制搜索时，最多会进行⌊logn⌋+1个递归调用，从而得到以下声明。

命题：对于有n个元素的排序数组，二进制搜索算法在O（logn）时间内运行。

理由：为了证明这一说法，一个关键的事实是，对于每个递归调用仍要搜索的候选元素的数量由该值给定

高-低+1。

此外，剩下的候选人人数至少减少了一半每个递归调用。具体来说，从mid的定义来看，剩余候选人的数量是

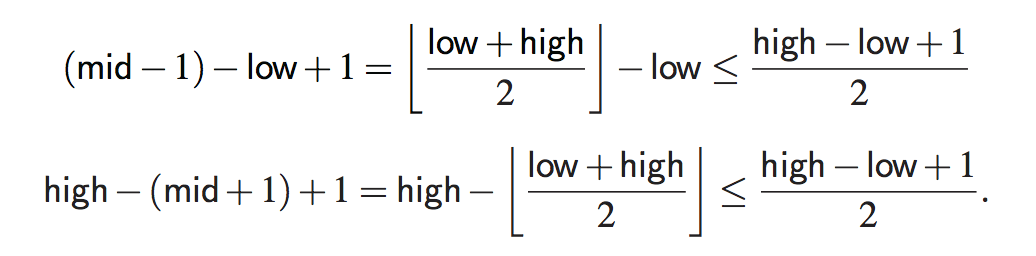
最初，候选数为n；在二进制搜索中，第一次调用后，最多为n/2；第二次调用后，最多为n/4；依此类推。一般来说，在二进制搜索的jth调用之后，剩余的候选元素的数目最多为n/2j。在最坏的情况下（搜索不成功），当不再有候选元素时，递归调用就会停止。因此，执行的最大递归调用数是最小的整数r，因此

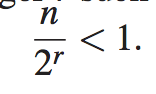
换句话说（回想一下，当对数的底是2时，我们省略了它），r是最小的整数，使得r>logn

r = ⌊log n⌋ + 1

这意味着二进制搜索在O（logn）时间内运行。

计算磁盘空间使用率

我们在上节中的最后一个递归算法是计算文件系统指定部分的总磁盘空间使用量。为了描述用于分析的“问题大小”，我们让n表示所考虑的文件系统部分中的文件系统条目数。

为了描述对diskUsage的初始调用所花费的累计时间，我们必须分析所进行的递归调用的总数，以及在这些调用中执行的操作数。

我们首先展示了该方法的精确n次递归调用，尤其是文件系统相关部分中的每个条目一次。直观地说，这是因为在处理包含e的唯一目录的条目时，仅在代码片段的for循环中对文件系统的特定条目e调用diskUsage，并且该条目只被探索一次。

为了形式化这个参数，我们可以定义每个条目的嵌套级别，使我们开始的条目具有嵌套级别0，直接存储在其中的条目具有嵌套级别1，存储在这些条目中的条目具有嵌套级别2，依此类推。我们可以通过归纳证明，在嵌套级别k的每个条目上，确实存在一次对diskUsage的递归调用。作为基本情况，当k=0时，唯一的递归调用是初始调用。作为归纳步骤，一旦我们知道在嵌套级别k的每个条目都有一次递归调用，我们就可以声明在嵌套级别k+1的每个条目e中只有一次调用，在包含e的k级条目的for循环中进行。

在确定文件系统的每个条目都有一个递归调用之后，我们回到算法的总计算时间问题上。如果我们可以争辩说我们在方法的任何一次调用中都花费了O（1）时间，那就太好了，但事实并非如此。在调用根部长度（）若要直接在该条目处计算磁盘使用量，当该条目是一个目录时，diskUsage方法的主体包含一个for循环，该循环遍历该目录中包含的所有条目。在最坏的情况下，一个条目可能包含n−1个其他条目。

基于这个推理，我们可以得出结论：存在O（n）递归调用，每个调用都在O（n）时间内运行，导致总体运行时间为O（n2）。虽然这个上限在技术上是正确的，但它不是一个严格的上限。值得注意的是，我们可以证明递归算法在O（n）时间内完成的强界！较弱的界限是悲观的，因为它假定每个目录的条目数是最坏的情况。虽然有些目录可能包含与n成比例的多个条目，但它们不可能都包含那么多。为了证明更有力的说法，我们选择考虑for循环在所有递归调用中的总迭代次数。我们声称整个循环中确实有n-1次这样的迭代。我们基于这样一个事实，即该循环的每次迭代都对diskUsage进行递归调用，但我们已经得出结论：总共有n个对diskUsage的调用（包括原始调用）。因此，我们得出结论：存在O（n）个递归调用，每个调用都在循环之外使用O（1）时间，并且由于循环而导致的操作总数是O（n）。将所有这些界限相加，运算的总数是O（n）。

我们提出的论点比以前的递归例子更先进。我们有时可以通过考虑累积效应来获得一系列操作的更严格的限制，而不是假设每个操作都达到最坏的情况，这是一种称为摊销的技术；此外，文件系统是一种被称为树的数据结构的隐式示例，而我们的磁盘使用算法实际上是一种更通用的树遍历算法的体现。树将是第8章的重点，我们关于磁盘使用算法的O（n）运行时间的讨论将在第8.4节中推广到树遍历。

递归的进一步例子

在本节中，我们将提供递归用法的其他示例。我们通过考虑可能从单个激活体中启动的最大递归调用数来组织演示。

• 如果一个递归调用最多启动一个，我们称之为线性递归。
• 如果一个递归调用可以启动另外两个调用，我们称之为二进制递归。
• 如果一个递归调用可能启动三个或多个其他调用，则这是多个递归。

线性递归

如果递归方法的设计使得对主体的每次调用最多进行一次新的递归调用，这就是所谓的线性递归。在我们目前看到的递归中，阶乘方法的实现是线性递归的一个明显例子。更有趣的是，二进制搜索算法也是线性递归的一个例子，尽管名称中有“二进制”一词。二进制搜索的代码包括一个案例分析，有两个分支会导致进一步的递归调用，但是在主体的特定执行过程中，只跟随一个分支。

线性递归定义的一个结果是，任何递归跟踪都将显示为单个调用序列，注意，线性递归术语反映了递归跟踪的结构，而不是运行时间的渐近分析；例如，我们已经看到二进制搜索在O（logn）时间内运行。

递归求数组元素的总和

线性递归是处理序列（如Java数组）的有用工具。例如，假设我们要计算一个n个整数数组的和。我们可以使用线性递归来解决这个求和问题，方法是观察如果n=0，则总和通常为0，否则它是数组中的前n−1个整数加上数组中最后一个值的和。

通过将最后一个数加到第一个n−1的和上，递归地计算序列的和。

基于这种直觉计算整数数组和的递归算法在代码中实现。

/∗∗ Returns the sum of the first n integers of the given array. ∗/
public static int linearSum(int[ ] data, int n) {
	if (n == 0)
		return 0;
	else
		return linearSum(data, n−1) + data[n−1];
}

下图给出了一个小例子的linearSum方法的递归轨迹。对于大小为n的输入，linearSum算法进行n+1方法调用。因为每次执行都会花费一部分时间。此外，我们还可以看到算法使用的内存空间（除了数组外）也是O（n），因为我们在进行最后一次递归调用（n=0）时，为跟踪中的n+1帧中的每个帧使用恒定数量的内存空间。

使用输入参数data=4、3、6、2、8执行linearSum（data，5）的递归跟踪。

以下递归视频讲解了递归算法的原理：