递归算法科普二

递归数据结构（结构递归）

递归在计算机科学中的一个重要应用是定义列表和树等动态数据结构。递归数据结构可以根据运行时需求动态地增长到理论上无限大的大小；相反，静态数组的大小必须在编译时设置。

当以递归的方式定义基础问题或待处理的数据时，递归算法特别适用。

本节中的示例说明了所谓的“结构递归”。这个术语指的是递归过程作用于递归定义的数据。

只要程序员从数据定义中派生模板，函数就采用结构递归。也就是说，函数体中的递归消耗给定复合值的一部分

Linked list 链接列表

下面是链接列表节点结构的C定义。特别注意如何根据自身定义节点。struct节点的next元素是指向另一个结构节点的指针，有效地创建了一个列表类型。

struct node
{
  int data;           // some integer data
  struct node *next;  // pointer to another struct node
};

因为struct-node数据结构是递归定义的，所以对其进行操作的过程可以自然地实现为递归过程。下面定义的list_print过程遍历列表，直到列表为空（即列表指针的值为NULL）。对于每个节点，它打印数据元素（一个整数）。在C实现中，列表由list_print过程保持不变。

void list_print(struct node *list)
{
    if (list != NULL)               // base case
    {
       printf ("%d ", list->data);  // print integer data followed by a space
       list_print (list->next);     // recursive call on the next node
    }
}

二叉树

下面是二叉树节点的简单定义。与链表的节点一样，它是根据自身递归地定义的。有两个自引用指针：left（指向左子树）和right（指向右子树）。

struct node
{
  int data;            // some integer data
  struct node *left;   // pointer to the left subtree
  struct node *right;  // point to the right subtree
};

树上的操作可以使用递归实现。请注意，由于有两个自引用指针（左和右），树操作可能需要两个递归调用：

// Test if tree_node contains i; return 1 if so, 0 if not.
int tree_contains(struct node *tree_node, int i) {
    if (tree_node == NULL)
        return 0;  // base case
    else if (tree_node->data == i)
        return 1;
    else
        return tree_contains(tree_node->left, i) || tree_contains(tree_node->right, i);
}

对于上面定义的tree_contains的任何给定调用，最多将进行两次递归调用。

// Inorder traversal:
void tree_print(struct node *tree_node) {
        if (tree_node != NULL) {                  // base case
                tree_print(tree_node->left);      // go left
                printf("%d ", tree_node->data);   // print the integer followed by a space
                tree_print(tree_node->right);     // go right
        }
}

上面的示例演示了按顺序遍历二叉树。二叉搜索树是二叉树的一种特殊情况，其中每个节点的数据元素都是按顺序排列的。

文件系统遍历

由于文件系统中的文件数量可能会有所不同，递归是遍历并枚举其内容的唯一实际方法。遍历文件系统与树遍历非常相似，因此树遍历背后的概念适用于遍历文件系统。更具体地说，下面的代码将是文件系统的预排序遍历的示例。

import java.io.*;

public class FileSystem {

	public static void main (String [] args) {
		traverse ();
	}

	/**
	 * Obtains the filesystem roots
	 * Proceeds with the recursive filesystem traversal
	 */
	private static void traverse () {
		File [] fs = File.listRoots ();
		for (int i = 0; i < fs.length; i++) {
			if (fs[i].isDirectory () && fs[i].canRead ()) {
				rtraverse (fs[i]);
			}
		}
	}

	/**
	 * Recursively traverse a given directory
	 *
	 * @param fd indicates the starting point of traversal
	 */
	private static void rtraverse (File fd) {
		File [] fss = fd.listFiles ();

		for (int i = 0; i < fss.length; i++) {
			System.out.println (fss[i]);
			if (fss[i].isDirectory () && fss[i].canRead ()) {
				rtraverse (fss[i]);
			}
		}
	}

}

这段代码混合了递归和迭代之间的行，至少在某种程度上是这样。它本质上是一种递归实现，这是遍历文件系统的最佳方法。它也是直接递归和间接递归的一个例子。方法rtraverse纯粹是一个直接示例；traverse是间接方法，它调用rtraverse。这个例子不需要“基本情况”场景，因为在给定的文件系统中总是有一些固定数量的文件或目录。

实施问题

在实际实现中，为了清晰或高效，可以进行一些修改，而不是纯粹的递归函数（基本情况的单个检查，否则是递归步骤）。其中包括：

• 包装器函数（在顶部）
• 短路基本情况，又名“公平合理的递归”（在底部）
• 混合算法（在底部）–一旦数据足够小，就切换到不同的算法

在优雅的基础上，包装器函数被普遍认可，而对基本情况进行短路则是不受欢迎的，特别是在学术界。在这种特殊情况下，递归算法通常是用来降低arm-length的开销的。

包装器函数

包装器函数是一个直接被调用但自身不递归的函数，而是调用一个单独的辅助函数来实际执行递归。

包装器函数可用于验证参数（因此递归函数可以跳过这些参数）、执行初始化（分配内存、初始化变量），特别是对于辅助变量（如“递归级别”或用于记忆的部分计算），以及处理异常和错误。在支持嵌套函数的语言中，辅助函数可以嵌套在包装函数中并使用共享范围。在没有嵌套函数的情况下，如果可能的话，辅助函数是一个单独的函数（因为它们不是直接调用的），并且通过使用传递引用与包装器函数共享信息。

基本情况短路

短路基本情况，也称为公平交易递归，包括在进行递归调用之前检查基本情况，即检查下一次调用是否为基本情况，而不是调用然后检查基本情况。短路特别是出于效率的考虑，以避免立即返回的函数调用的开销。注意，由于已经检查了基本用例（在递归步骤之前），因此不需要单独检查它，但是当整个递归从基本用例本身开始时，确实需要对该用例使用包装器函数。例如，在阶乘函数中，基本情况是0！=1，同时立即为1返回1！是短路，可能会漏掉0；这可以通过包装函数来缓解。

当遇到许多基本情况时，短路主要是一个问题，例如树中的空指针，它在函数调用的数量上可能是线性的，因此O（n）算法的显著节省；下面将对深度优先搜索进行说明。树上的短路对应于将叶（没有子节点的非空节点）视为基本情况，而不是将空节点视为基本情况。如果只有一个基本情况，例如在计算阶乘时，短路只提供O（1）节省。

从概念上讲，短路可以被视为具有相同的基本情况和递归步骤，只在递归之前检查基本情况，或者可以将其视为具有不同的基本情况（从标准基本情况中删除一个步骤）和一个更复杂的递归步骤，即“检查有效然后递归”，就像在考虑叶节点一样而不是将空节点作为树中的基本情况。由于短路有一个更复杂的流程，与标准递归中基本情况和递归步骤的明确分离相比，它常常被认为是糟糕的风格。

深度优先搜索

在二叉树的深度优先搜索（DFS）中给出了短路的一个基本示例；有关标准递归讨论，请参阅“二叉树”一节：https://javakk.com/532.html

DFS的标准递归算法是：

• 基本情况：如果当前节点为Null，则返回false
• 递归步骤：否则，检查当前节点的值，如果匹配则返回true，否则在子节点上递归

在短路时，这是：

• 检查当前节点的值，如果匹配则返回true，
• 否则，在子级上，如果不为Null，则递归。

就标准步骤而言，这会将基本情况检查移到递归步骤之前。或者，可以将它们分别视为基本情况和递归步骤的不同形式。请注意，这需要一个包装函数来处理树本身为空（根节点为Null）的情况。

在高度为h的完美二叉树的情况下，有2h+1−1节点和2h+1空指针作为子级（每个2h离开2个），因此在最坏的情况下，短路会将函数调用的数量减少一半。

在C语言中，标准递归算法可以实现为：

bool tree_contains(struct node *tree_node, int i) {
    if (tree_node == NULL)
        return false;  // base case
    else if (tree_node->data == i)
        return true;
    else
        return tree_contains(tree_node->left, i) ||
               tree_contains(tree_node->right, i);
}

短路算法可以实现为：

// Wrapper function to handle empty tree
bool tree_contains(struct node *tree_node, int i) {
    if (tree_node == NULL)
        return false;  // empty tree
    else
        return tree_contains_do(tree_node, i);  // call auxiliary function
}

// Assumes tree_node != NULL
bool tree_contains_do(struct node *tree_node, int i) {
    if (tree_node->data == i)
        return true;  // found
    else  // recurse
        return (tree_node->left  && tree_contains_do(tree_node->left,  i)) ||
               (tree_node->right && tree_contains_do(tree_node->right, i));
}

注意使用了对布尔&&（AND）运算符的短路求值，因此只有在节点有效（非空）时才进行递归调用。请注意，虽然AND中的第一个项是指向节点的指针，但第二个项是bool，因此整个表达式的计算结果为bool。这是递归短路中的一个常见习语。这是对布尔| |（OR）运算符的短路求值的补充，仅在左子运算符失败时检查右子项。实际上，这些函数的整个控制流可以用return语句中的一个布尔表达式来代替，但是易读性对效率没有任何好处。

混合算法

由于重复函数调用和返回的开销，递归算法对于小数据通常效率低下。因此，递归算法的有效实现通常从递归算法开始，但是当输入变小时，就切换到另一种算法。一个重要的例子是合并排序，当数据足够小时，通常通过切换到非递归插入排序来实现，如平铺合并排序。混合递归算法通常可以进一步细化，如在Timsort中，它是从混合的合并排序/插入排序派生出来的。

递归与迭代

递归和迭代的表现力是一样的：递归可以用显式调用堆栈的迭代代替，而迭代可以用尾部递归代替。哪种方法更可取取决于所考虑的问题和所使用的语言。在命令式编程中，迭代是首选，特别是对于简单递归，因为它避免了函数调用和调用堆栈管理的开销，但递归通常用于多个递归。相反，在函数式语言中，递归是首选的，尾部递归优化导致的开销很小。使用迭代实现算法可能不容易实现。

比较模板以计算xbase中xn=f（n，xn-1）定义的xn：

function recursive(n)
    if n == base
        return xbase
    else
        return f(n, recursive(n-1)) 

function iterative(n)
    x = xbase
    for i = base+1 to n
        x = f(i, x)
    return x

对于命令式语言，开销是定义函数，对于函数式语言，开销是定义累加器变量x。

例如，阶乘函数可以通过赋值给循环索引变量和累加器变量，而不是通过递归传递参数和返回值，在C中迭代实现：

unsigned int factorial(unsigned int n) {
  unsigned int product = 1; // empty product is 1
  while (n) {
    product *= n;
    --n;
  }
  return product;
}

表现力

现在使用的大多数编程语言都允许直接指定递归函数和过程。当调用这样的函数时，程序的运行时环境会跟踪该函数的各种实例（通常使用调用堆栈，但也可能使用其他方法）。通过用迭代控制结构替换递归调用，并用程序显式管理的堆栈模拟调用堆栈，可以将每个递归函数转换为迭代函数

相反，所有可由计算机评估的迭代函数和过程（参见图灵完全性）都可以用递归函数来表示；迭代控制结构，如while循环和for循环，都是用函数语言以递归形式重写的。然而，实际上，这种重写依赖于尾部调用的消除，这并不是所有语言的特性。C、 Java和Python是值得注意的主流语言，在这些语言中，所有函数调用（包括尾部调用）都可能导致使用循环结构时不会发生的堆栈分配；在这些语言中，以递归形式重写的可工作迭代程序可能会溢出调用堆栈，尽管尾部调用消除可能是一个特性不在语言规范中，并且同一语言的不同实现可能在尾部调用消除功能上有所不同。

性能问题

在支持迭代循环构造的语言（如C和Java）中，由于管理堆栈所需的开销和函数调用的相对缓慢性，通常与递归程序相关的时间和空间开销很大；在函数式语言中，函数调用（尤其是尾部调用）通常是一个非常快速的操作，并且这种差异通常不太明显。

作为一个具体的例子，上面“factorial”示例的递归和迭代实现之间的性能差异很大程度上取决于所使用的编译器。在优先使用循环结构的语言中，迭代版本可能比递归版本快几个数量级。在函数式语言中，这两个实现的总时间差可以忽略不计；事实上，首先乘以较大的数字而不是较小的数字（这里给出的迭代版本正好是这样）的成本可能会压倒通过选择迭代节省的任何时间。

堆栈空间

在某些编程语言中，调用堆栈的最大大小远远小于堆中的可用空间，递归算法往往比迭代算法需要更多的堆栈空间。因此，这些语言有时会限制递归的深度以避免堆栈溢出；Python就是这样一种语言。注意下面关于尾部递归的特殊情况的警告。

https://javakk.com/521.html

脆弱性

由于递归算法可能会受到堆栈溢出的影响，因此它们可能容易受到病态或恶意输入的攻击。一些恶意软件专门针对程序的调用堆栈，并利用堆栈固有的递归特性。即使在没有恶意软件的情况下，无限递归导致的堆栈溢出对程序来说可能是致命的，异常处理逻辑可能无法阻止相应的进程终止。

多重递归问题

多重递归问题本质上是递归的，因为它们需要跟踪先验状态。一个例子是树遍历作为深度优先搜索；虽然使用递归和迭代方法，它们与列表遍历和列表中的线性搜索相比，后者是一种单独递归的自然迭代方法。其他示例包括分而治之算法（如快速排序）和函数（如Ackermann函数）。所有这些算法都可以在显式堆栈的帮助下迭代实现，但是程序员管理堆栈所付出的努力，以及由此产生的程序的复杂性，可以说超过了迭代解决方案的任何优势。

重构递归

递归算法可以替换为非递归算法。替代递归算法的一种方法是使用堆内存代替堆栈内存来模拟它们。另一种方法是开发完全基于非递归方法的替换算法，这可能很有挑战性。例如，递归算法匹配通配符，例如Rich Salz的wildmat算法曾经是典型的。出于同样目的的非递归算法，例如Krauss匹配通配符算法，已经被开发出来以避免递归的缺点，并且只是在收集测试和分析性能等技术的基础上逐步改进的。

尾部递归函数

尾部递归函数是所有递归调用都是尾部调用的函数，因此不构建任何延迟操作。例如，gcd函数（如下所示）是尾部递归的。相反，factorial函数（如下所示）不是tail recursive；因为它的递归调用不在tail位置，它建立了延迟的乘法操作，这些操作必须在最终递归调用完成后执行。对于将尾部递归调用视为跳转而不是函数调用的编译器或解释器，尾部递归函数（如gcd）将使用常量空间执行。因此，程序本质上是迭代的，相当于使用命令式语言控制结构，如“for”和“while”循环。

//INPUT: Integers x, y such that x >= y and y >= 0
int gcd(int x, int y)
{
  if (y == 0)
     return x;
  else
     return gcd(y, x % y);
}

//INPUT: n is an Integer such that n >= 0
int fact(int n)
{
   if (n == 0)
      return 1;
   else
      return n * fact(n - 1);
}

尾部递归的意义在于，当进行尾部递归调用（或任何尾部调用）时，调用方的返回位置不必保存在调用堆栈上；当递归调用返回时，它将直接在先前保存的返回位置上分支。因此，在识别尾部调用这一属性的语言中，尾部递归既节省了空间又节省了时间。

执行命令

在函数只调用自身一次的简单情况下，在递归调用之前的指令在递归调用之后的任何指令之前，每次递归执行一次。后者在达到最大递归后重复执行。考虑这个例子：

功能1：

void recursiveFunction(int num) {
   printf("%d\n", num);
   if (num < 4)
      recursiveFunction(num + 1);
}

带交换线的功能2：

void recursiveFunction(int num) {
   if (num < 4)
      recursiveFunction(num + 1);
   printf("%d\n", num);
}

递归算法的时间效率

递归算法的时间效率可以用大O符号的递推关系来表示。它们可以（通常）简化成一个大的O项。

捷径法则（主定理）

如果函数的时间复杂性为

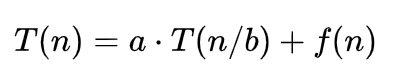
因此，时间复杂度的大O是：

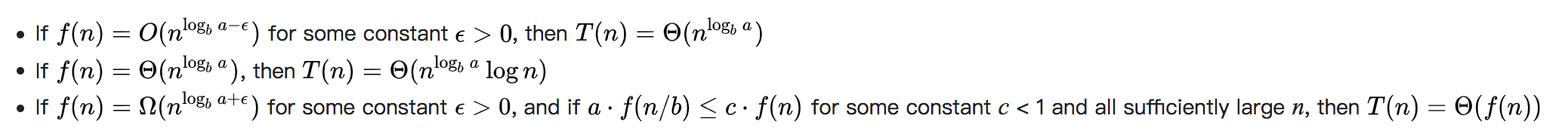
其中，a表示每一级递归的递归调用数，b表示下一级递归的输入的较小因子（即，将问题分解成的块数），f （n）表示函数独立于任何递归所做的工作（例如分区，重新组合）在每一级递归。

同样可以参考这篇文章：https://javakk.com/508.html