Java递归函数与算法讲解系列一

在计算机程序中描述重复的一种方法是使用循环，如Java的while循环和for循环结构。实现重复的完全不同的方法是通过一个称为递归的过程。

递归是一种方法对自身进行一次或多次调用的技术，在执行期间，或数据结构依赖于同一类型的结构。有很多例子艺术与自然中的递归。例如，分形图案是自然递归的。艺术中使用递归的物理例子是俄罗斯的Matryoshka玩偶。每个玩偶要么是实木做的，要么是空心的，里面装着另一个奶嘴里面有洋娃娃。

在计算中，递归为执行重复性任务提供了一种优雅而强大的选择。实际上，一些编程语言（例如Scheme，Smalltalk）不显式支持循环构造，而是直接依赖关于表示重复的递归。大多数现代编程语言都支持函数递归，使用与支持传统形式的方法调用相同的机制。当调用，则该调用将挂起，直到递归调用完成。

递归是数据结构研究中的一项重要技术。我们将在本书后面几章中重点使用它。在系列中，我们从以下四个使用递归的示例开始，为每个示例提供了一个Java实现。

• 阶乘函数（通常表示为n！）是一个经典的数学具有递归定义的自然函数。
• 英国尺子具有递归模式，这是分形的一个简单示例结构。
• 二进制搜索是最重要的计算机算法之一。它允许以高效地定位我们需要的数十亿个数据集条目的数量。
• 计算机的文件系统具有递归结构，其中目录可以任意深入嵌套在其他目录中。递归算法被广泛用于探索和管理这些文件系统。

然后，我们将描述如何对递归算法，我们讨论了定义递归时的一些潜在陷阱。在本章的最后，我们提供了更多递归的例子算法，组织起来突出一些常见的设计形式。

递归示例

阶乘函数

为了演示递归机制，我们从一个简单的数学开始计算阶乘函数值的示例。正整数n的阶乘，用n表示！，定义为从1到n的整数的乘积。如果n=0，然后n！按惯例定义为1。更正式地说，对于任何n≥0的整数

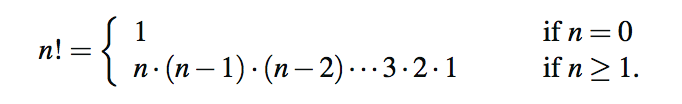
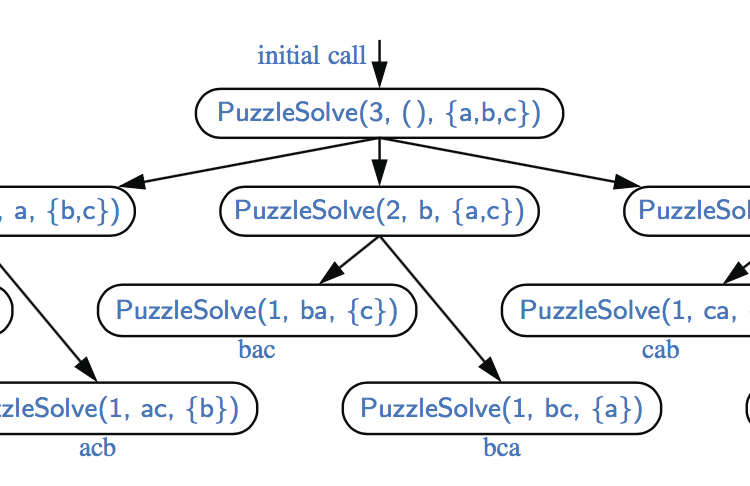
例如，5！=5·4·3·2·1=120。阶乘函数很重要，因为众所周知，它等于n个不同项目的排列方式变成一个序列，即n个项目的排列数。例如 a、b、c 三个字可以排成 3! = 3 · 2 · 1 = 6 ways: abc、acb、bac、bca、cab、cba。

阶乘函数有一个自然的递归定义。看到这个，注意5！=5·（4·3·2·1）=5·4！。更一般地说，对于正整数n，我们可以定义n！变成n·（n−1）！。这个递归定义可以形式化为

这个定义是许多函数递归定义中的典型定义。首先，我们有一个或多个基本情况，它们引用函数的固定值。以上定义有一个基本情况说明n！对于n=1。第二，我们有一个或者更递归的情况，根据函数本身定义函数。在上面定义中，有一个递归的例子，它表示n！=n·（n−1）！对于n≥1。

一个递归函数的实现

我们不能用递归的数学符号来设计factorial函数的实现：

public static int factorial(int n) throws IllegalArgumentException {
	if (n < 0)
		throw new IllegalArgumentException( ); // argument must be nonnegative
	else if (n == 0)
		return 1; // base case
	else
		return n ∗ factorial(n−1); // recursive case
}

此方法不使用任何显式循环。重复是通过方法的重复递归调用。这个过程是有限的，因为每个当方法被调用时，它的参数会变小一个，则不再进行递归调用。

我们演示了使用递归跟踪执行递归方法。每个跟踪项对应于递归调用。每次新的递归方法调用由指向新调用的向下箭头指示。当方法返回时，将绘制一个显示此返回值的箭头，并且返回值可以在该箭头旁边指示。阶乘函数的这种跟踪的示例如所示：

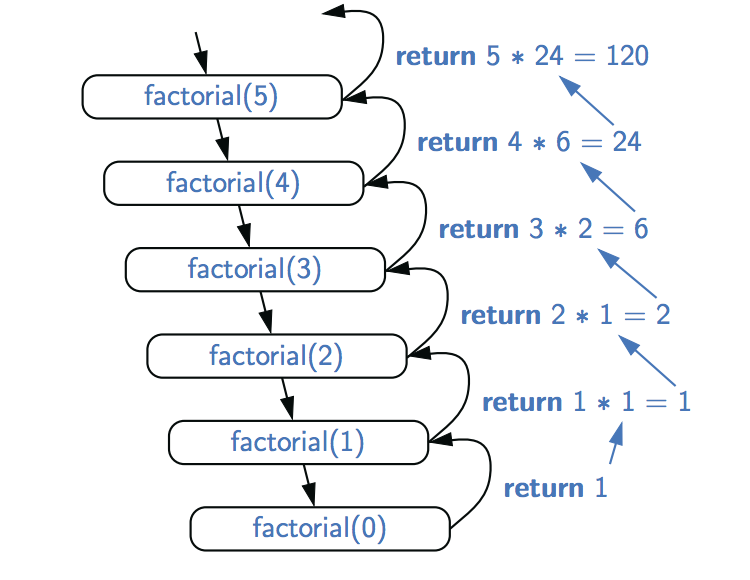
递归跟踪紧密地反映了编程语言对递归的执行。在Java中，每次调用一个方法（递归的或其他的）时，都会创建一个称为激活记录或激活帧的结构来存储有关该方法调用进度的信息。此框架存储特定于方法的给定调用的参数和局部变量，以及有关方法主体中当前正在执行的命令的信息。

当一个方法的执行导致一个嵌套方法调用时，前一个调用的执行被挂起，并且它的框架存储源代码中在返回嵌套调用时控制流应该继续的位置。然后为嵌套方法调用创建一个新的框架。此过程既可用于一个方法调用另一个方法的标准情况，也可用于方法调用自身的递归情况。关键点是每个活动呼叫都有一个单独的帧。

下面是阶乘递归算法的视频讲解：

也可以参考这篇递归算法讲解的文章：https://javakk.com/626.html

画英国尺子

在计算阶乘函数的情况下，没有令人信服的理由比循环直接迭代更喜欢递归。作为使用递归的一个更复杂的例子，考虑一下如何绘制典型英国尺子的标记。对于每一英寸，我们都会用数字标签打勾。我们表示刻度的长度，表示整个英寸作为主要刻度长度。在表示整英寸的标记之间，标尺包含一系列小刻度，间隔为1/2英寸、1/4英寸，依此类推。当间隔的大小减少一半时，记号长度将减少1。图5.2展示了几种主要刻度长度不同的标尺（尽管没有按比例绘制）。

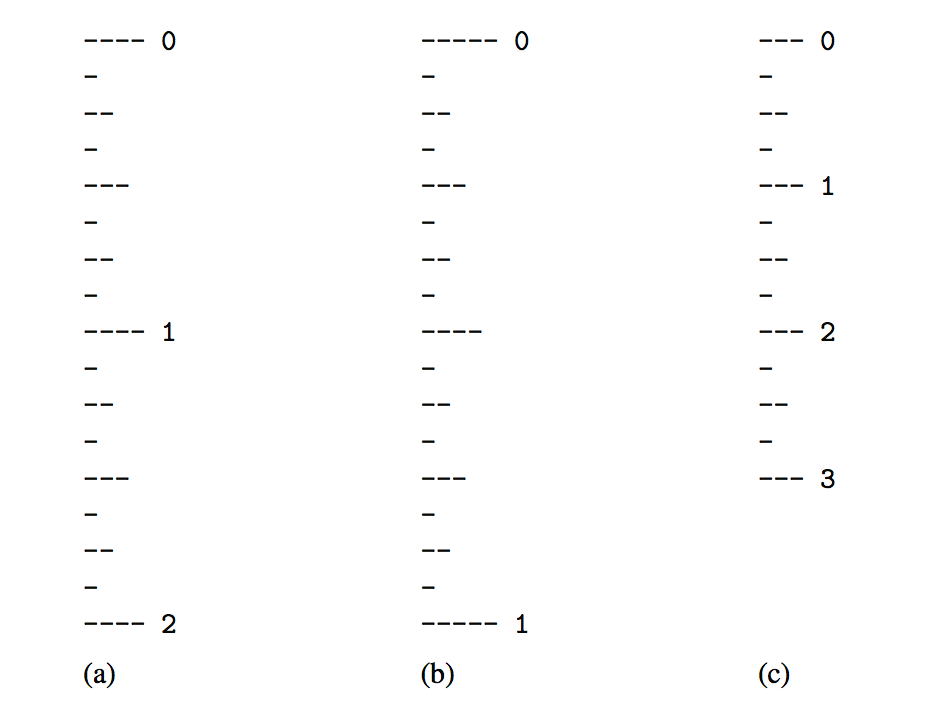
递归作图法

一个简单的，具有各种层次的分形结构。考虑图上图所示的主刻度长度为5的规则。忽略包含0和1的行，让我们考虑如何绘制位于这两行之间的记号序列。中央的滴答声（1/2英寸）的长度是4。请注意，这个中央记号上方和下方的两个记号图案是相同的，并且每一个都有一个长度为3的中央记号。

一般来说，中心刻度长度L≥1的间隔由以下组成：

• 中心刻度长度L−1的间隔
• 长度为L的单个刻度
• 中心刻度长度L−1的间隔

虽然可以使用迭代过程绘制这样一个标尺，但使用递归可以更容易地完成任务。我们的实现包括三个方法。

主要的方法，drawRuler，管理整个标尺的构造。它的参数指定标尺的总英寸数和主刻度长度。实用方法drawLine使用指定数量的短划线（以及打印在记号右侧的可选整数标签）绘制单个记号。

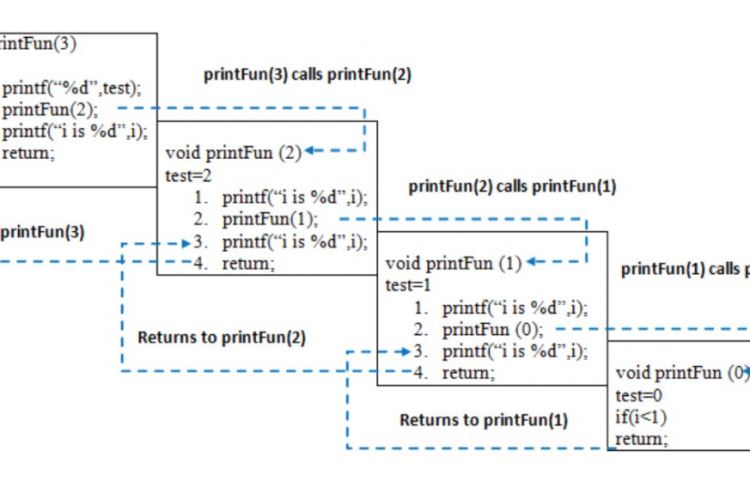
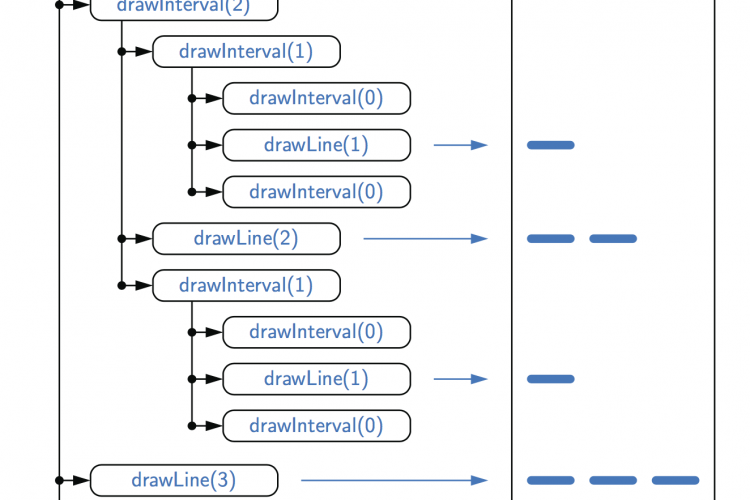
有趣的工作是用递归drawininterval方法完成的。此方法根据间隔中心刻度的长度绘制某个间隔内的次要刻度序列。我们依赖于本页顶部所示的直觉，以及当L=0时什么也不画的基本情况。对于L≥1，第一步和最后一步通过递归调用drawInterval（L−1）来执行。中间步骤通过调用方法drawLine（L）来执行。

/∗∗ Draws an English ruler for the given number of inches and major tick length. ∗/
public static void drawRuler(int nInches, int majorLength) {
	drawLine(majorLength, 0); // draw inch 0 line and label
	for (int j = 1; j <= nInches; j++) {
		drawInterval(majorLength − 1); // draw interior ticks for inch
		drawLine(majorLength, j); // draw inch j line and label
	}
}
private static void drawInterval(int centralLength) {
	if (centralLength >= 1) { // otherwise, do nothing
		drawInterval(centralLength − 1); // recursively draw top interval
		drawLine(centralLength); // draw center tick line (without label)
		drawInterval(centralLength − 1); // recursively draw bottom interval
	}
}
private static void drawLine(int tickLength, int tickLabel) {
	for (int j = 0; j < tickLength; j++)
		System.out.print("-");
		if (tickLabel >= 0)
		System.out.print(" " + tickLabel);
		System.out.print("\n");
}
/∗∗ Draws a line with the given tick length (but no label). ∗/
private static void drawLine(int tickLength) {
	drawLine(tickLength, −1);
}