Java递归算法讲解一

从另一个函数调用一个函数的想法立即暗示了函数调用自身的可能性。Java中的函数调用机制支持这种可能性，即递归。

下面这个视频通过代码讲述了递归的基本原理：

递归算法示例

递归的“Hello，World”是阶乘函数，它是由等式为正整数n定义的

public class Factorial {

    // return n!
    // precondition: n >= 0 and n <= 20
    public static long factorial(long n) {
        if      (n <  0) throw new RuntimeException("Underflow error in factorial");
        else if (n > 20) throw new RuntimeException("Overflow error in factorial");
        else if (n == 0) return 1;
        else             return n * factorial(n-1);
    }

    public static void main(String[] args) {
        long n = Long.parseLong(args[0]);
        StdOut.println(factorial(n));
    }

}

数量n！使用以下递归函数：

public static long factorial(int n) { 
    if (n == 1) return 1; 
    return n * factorial(n-1); 
} 

我们可以像跟踪任何函数调用序列一样精确地跟踪这个计算。

factorial(5) 
   factorial(4) 
      factorial(3) 
         factorial(2) 
            factorial(1) 
               return 1 
            return 2*1 = 2 
         return 3*2 = 6 
      return 4*6 = 24 
   return 5*24 = 120

factorial()实现展示了每个递归函数所需的两个主要组件。

• 基本情况返回一个值，而不进行任何后续递归调用。对于一个或多个递归函数，可以对它求值。对于factorial()，基本情况为n=1。
• 归约步骤是递归函数的核心部分。它将函数在一个（或多个）输入值处的值与函数在一个（或多个）其他输入值处的值相关联。此外，输入值的序列值必须收敛到基本情况。对于factorial()，每次调用n的值都会减少1，因此输入值序列会收敛到基本情况。

数学归纳法

递归编程与数学归纳法直接相关，数学归纳法是一种证明自然数事实的技术。用数学归纳法证明一个包含整数n的语句对无穷多个n值是真的，包括以下两个步骤：

• 基本情况：对于某些特定值或n的值（通常为0或1），证明语句为真。
• 归纳步骤：假设所有小于n的正整数的陈述都是真的，然后用这个事实来证明它对于n是真的。

这样的证明足以证明该语句对n的无穷多个值是真的：我们可以从基本情况开始，然后用我们的证明来证明对于n的每一个较大值，该语句都是真的。

欧几里得算法

两个正整数的最大公约数（gcd）是平均分为两个正整数的最大整数。例如，gcd（102，68）=34。

我们可以使用以下属性有效地计算gcd，该属性适用于正整数p和q：

如果 p>q，p 和 q 的 gcd 与 q 和 p%q 的 gcd 相同。

public class Euclid {

    // recursive implementation
    public static int gcd(int p, int q) {
        if (q == 0) return p;
        else return gcd(q, p % q);
    }

    // non-recursive implementation
    public static int gcd2(int p, int q) {
        while (q != 0) {
            int temp = q;
            q = p % q;
            p = temp;
        }
        return p;
    }

    public static void main(String[] args) {
        int p = Integer.parseInt(args[0]);
        int q = Integer.parseInt(args[1]);
        int d  = gcd(p, q);
        int d2 = gcd2(p, q);
        StdOut.println("gcd(" + p + ", " + q + ") = " + d);
        StdOut.println("gcd(" + p + ", " + q + ") = " + d2);
    }
}

gcd(1440, 408) 
   gcd(408, 216) 
      gcd(216, 192) 
         gcd(192, 24)
            gcd(24, 0)
               return 24
            return 24 
         return 24 
      return 24 
   return 24 

河内塔楼

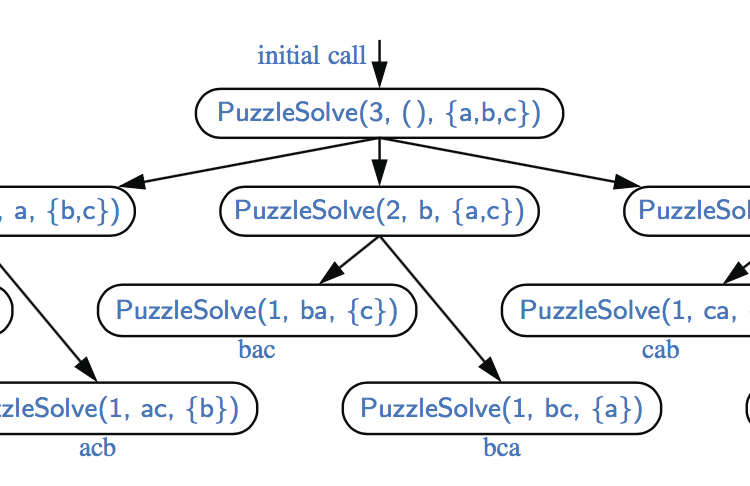
汉诺塔问题的递推解法在汉诺塔问题中，我们有三个极点和n个圆盘，它们与极点相吻合。这些圆盘大小不同，最初堆放在其中一个磁极上，从底部最大的（圆盘n）到顶部最小的（圆盘1）。任务是将所有n个圆盘移动到另一个极点，同时遵守以下规则：

• 一次只能移动一张光盘。
• 不要把大碟片放在小碟片上。

public class TowersOfHanoi {

    // print out instructions for moving n discs to
    // the left (if left is true) or right (if left is false)
    public static void moves(int n, boolean left) {
        if (n == 0) return;
        moves(n-1, !left);
        if (left) StdOut.println(n + " left");
        else      StdOut.println(n + " right");
        moves(n-1, !left);
    }

    public static void main(String[] args) {
        int n = Integer.parseInt(args[0]);
        moves(n, true);
    }

}

递归正好提供了我们需要的计划：首先我们将顶部的n−1个圆盘移动到一个空极，然后将最大的圆盘移动到另一个空极，然后通过将n−1个圆盘移动到最大的圆盘上来完成这项工作。

更多递归算法科普可以参考这篇文章：https://javakk.com/532.html

指数时间

指数增长let T（n）是由发出的移动指令数汉诺瓦塔TowersOfHanoi把n个圆盘从一个销子移到另一个。那么，T（n）必须满足以下等式：

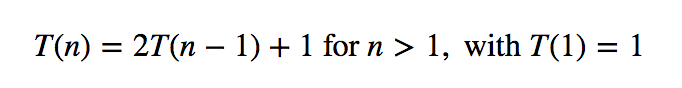
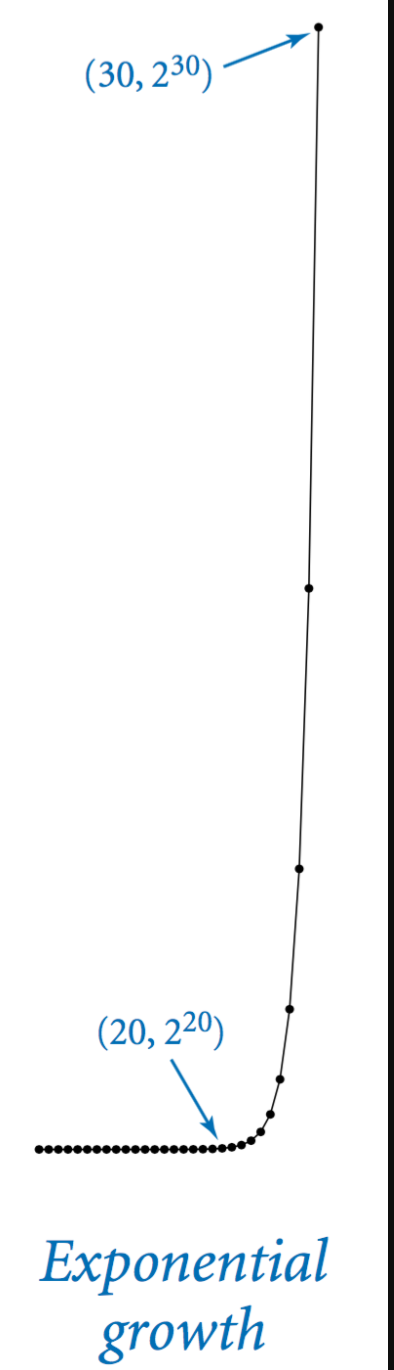
这种方程在离散数学中被称为递推关系。我们通常可以用它们来导出感兴趣量的闭式表达式。例如，T（1）=1，T（2）=3，T（3）=7，T（4）=15。一般来说，T（n）=2n−1。假设僧侣们以每秒一个的速度移动圆盘，他们需要58亿个世纪才能解决64个圆盘的问题。

灰色代码

n位格雷码是2n个不同的n位二进制数的列表，这样列表中的每个条目与它的前一个条目精确地相差一位。n位二进制反射格雷码递归定义如下：

• n−1位代码，每个字前加0，后跟
• 以相反顺序排列的n−1位代码，每个字前加1。

0位代码被定义为空，因此1位代码是0后跟1。

public class Beckett {

    public static void moves(int n, boolean forward) {
        if (n == 0) return;
        moves(n-1, true);
        if (forward) StdOut.println("enter " + n);
        else         StdOut.println("exit  " + n);
        moves(n-1, false);
    }

    public static void main(String[] args) {
        int n = Integer.parseInt(args[0]);
        moves(n, true);
    }

}

使用n位灰色代码为n个字符的播放打印舞台指示，以便角色一次进入和退出一个，以便舞台上的每个角色子集只出现一次。

递归图形

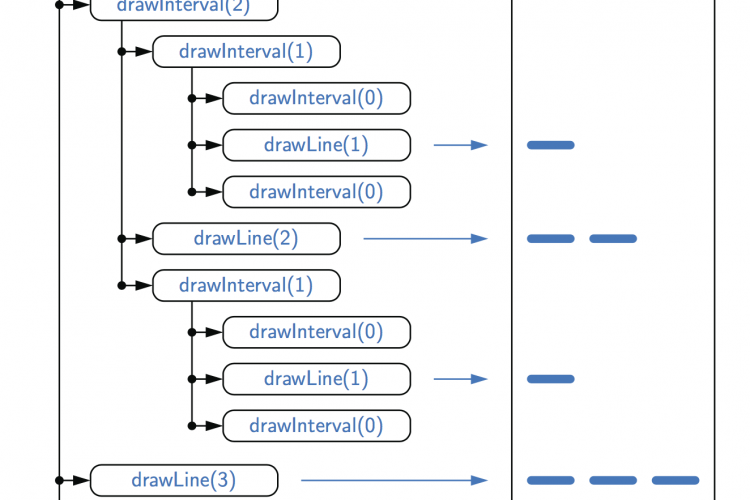
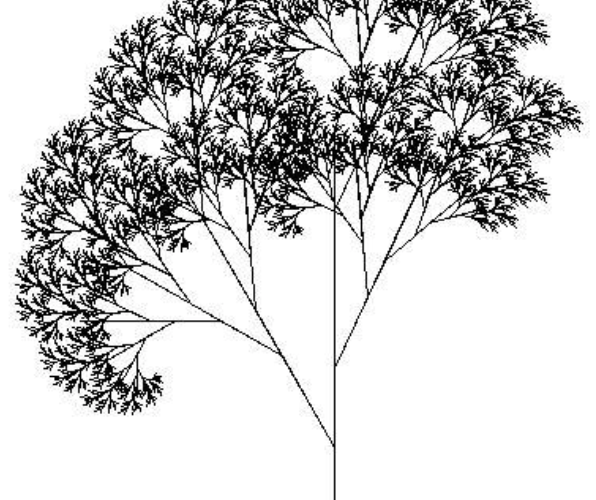
简单的递归绘图方案可以生成非常复杂的图片。例如，n阶H-树的定义如下：n=0的基本情况为null。简化步骤是在单位正方形内画出字母H形状的三条线，四棵n−1级的H-树，一条连接到H的每个尖端，附加条件是n−1级的H-树在正方形的四个象限中居中，大小减半。

public class Htree {

    // plot an H, centered on (x, y) of the given side length
    public static void drawH(double x, double y, double size) {

        // compute the coordinates of the 4 tips of the H
        double x0 = x - size/2;
        double x1 = x + size/2;
        double y0 = y - size/2;
        double y1 = y + size/2;

        // draw the 3 line segments of the H
        StdDraw.line(x0, y0, x0, y1);    // left  vertical segment of the H
        StdDraw.line(x1, y0, x1, y1);    // right vertical segment of the H
        StdDraw.line(x0,  y, x1,  y);    // connect the two vertical segments of the H
    }

    // plot an order n H-tree, centered on (x, y) of the given side length
    public static void draw(int n, double x, double y, double size) {
        if (n == 0) return;
        drawH(x, y, size);

        // compute x- and y-coordinates of the 4 half-size H-trees
        double x0 = x - size/2;
        double x1 = x + size/2;
        double y0 = y - size/2;
        double y1 = y + size/2;

        // recursively draw 4 half-size H-trees of order n-1
        draw(n-1, x0, y0, size/2);    // lower left  H-tree
        draw(n-1, x0, y1, size/2);    // upper left  H-tree
        draw(n-1, x1, y0, size/2);    // lower right H-tree
        draw(n-1, x1, y1, size/2);    // upper right H-tree
    }

    // reads an integer command-line argument n and plots an order n H-tree
    public static void main(String[] args) {
        int n = Integer.parseInt(args[0]);

        double x = 0.5, y = 0.5;   // center of H-tree
        double size = 0.5;         // side length of H-tree
        draw(n, x, y, size);
    }
}

取一个命令行参数n，并在标准绘图中绘制n阶的H-树。H-树是分形的一个简单示例：一个可以分成多个部分的几何图形，每个部分（大约）都是原始形状的缩小副本。