Java递归方法Recursive详解

sofia 4年前 (2020-10-04) Java系列 | 抢沙发 1353

文章评分 0 次，平均分 0.0 ：

我们探索一个方法可以做的最神奇的事情之一：调用自身来解决同一问题的较小版本。调用自身的方法称为递归方法。

递归Void方法

考虑以下示例：

public static void countdown(int n) {
    if (n == 0) {
        System.out.println("Blastoff!");
    } else {
        System.out.println(n);
        countdown(n - 1);
    }
}

方法的名称是countdown；它接受单个整数作为参数。如果参数为0，则显示单词blatoff！。否则，它将显示数字，然后调用自己，并将n-1作为参数传递。

如果我们从main调用倒计时（3），会发生什么？

倒计时的执行从n==3开始，由于n不是0，它显示值3，然后调用自己。。。

	倒计时的执行从n==2开始，由于n不是0，它显示值2，然后调用自己。。。

		倒计时的执行从n==1开始，由于n不是0，它显示值1，然后调用自己。。。

			倒计时的执行从n==0开始，由于n是0，它显示单词Blastoff！然后回来。

		得到n==1的倒计时返回。

	得到n==2的倒计时返回。

得到n==3的倒计时返回。

然后你又回来了。总输出结果如下：

3
2
1
Blastoff!

第二个例子

public static void newLine() {
    System.out.println();
}

public static void threeLine() {
    newLine();
    newLine();
    newLine();
}

虽然这些方法有效，但是如果我们想显示两个换行符，或者可能是100个换行符，它们也没有帮助。更普遍的选择是：

public static void nLines(int n) {
    if (n > 0) {
        System.out.println();
        nLines(n - 1);
    }
}

此方法以整数n作为参数，并显示n个换行符。结构类似于倒计时。只要n大于0，它就会显示一个新行，然后调用自己来显示（n−1）个额外的新行。新行的总数是1+（n-1），这正是我们想要的：n。

递归堆栈图

我们使用堆栈图来表示方法调用期间程序的状态。同样的图表可以使递归方法的解释更容易。

请记住，每次调用方法时，Java都会创建一个新的框架，其中包含该方法的参数和变量。图8.1是倒计时的堆栈图，用n==3调用。

Java递归方法Recursive详解

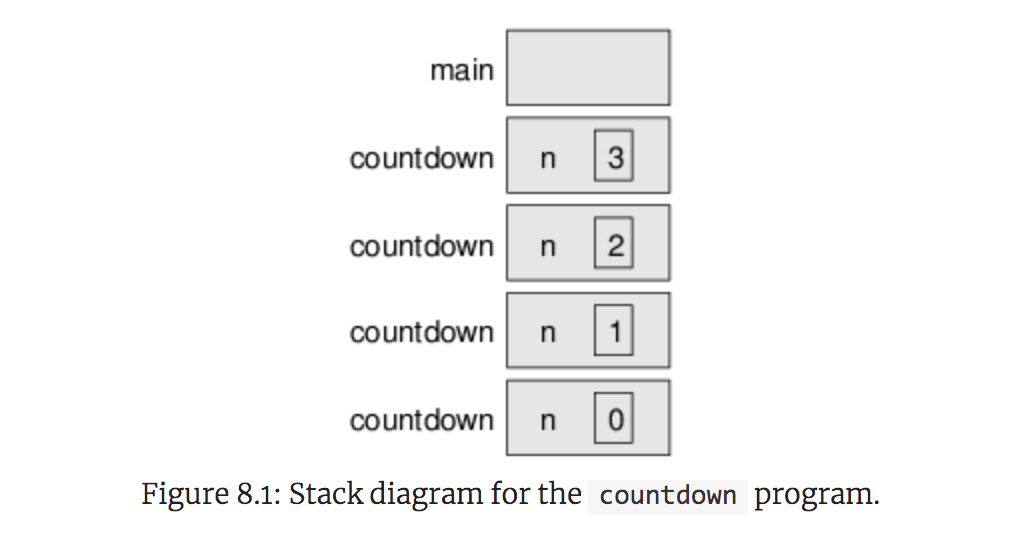
按照惯例，main的帧在顶部，其他帧的堆栈向下增长。这样，我们就可以在纸上绘制堆栈图，而无需猜测它们将增长到什么程度。main的框架为空，因为main没有任何变量。（它有参数args，但由于我们没有使用它，所以我们将其排除在图表之外。）

倒计时有四个帧，每个帧的参数n都有不同的值。最后一帧n==0，称为基本情况。它不进行递归调用，因此它下面没有更多的帧。

如果递归方法中没有基本情况，或者从未达到基本情况，堆栈将永远增长，至少在理论上是这样。实际上，堆栈的大小是有限的。如果超过限制，就会出现 stackoverflower

例如，下面是一个没有基本情况的递归方法：

public static void forever(String s) {
    System.out.println(s);
    forever(s);
}

此方法显示给定的字符串，直到堆栈溢出为止，此时它抛出一个错误。在你的计算机上试试这个例子，你可能会惊讶于错误消息的长度！

值返回方法

为了让您了解如何使用所学的工具进行操作，让我们看看对递归定义的数学函数求值的方法。

递归定义与“循环”定义类似，定义指的是被定义的事物。当然，真正的循环定义并不是很有用：

递归：

用于描述递归方法的形容词。

如果你在字典里看到这个定义，你可能会生气。再次，如果你在谷歌上搜索“递归”，它会显示“你的意思是：递归”是一个内部笑话。人们总是喜欢这种联系。

许多数学函数都是递归定义的，因为这通常是最简单的方法。例如，一个整数n的阶乘，它写为n！，定义如下：

0！=1

n！=n·（n−1）！

不要混淆数学符号！，表示阶乘，使用Java运算符！，意思是没有。这个定义表示阶乘（0）是1，阶乘（n）是n*阶乘（n-1）。

所以阶乘（3）是3*阶乘（2）；阶乘（2）是2*阶乘（1）；阶乘（1）是1*阶乘（0）；阶乘（0）是1。综合起来，我们得到3*2*1*1，就是6。

如果您可以为某个事物制定递归定义，那么就可以轻松地编写一个Java方法来计算它。第一步是确定参数和返回类型。因为factorial是为整数定义的，所以该方法接受int作为参数并返回int：

public static int factorial(int n) {
    return 0;  // stub
}

接下来，我们考虑基本情况。如果参数恰好为0，则返回1:

public static int factorial(int n) {
    if (n == 0) {
        return 1;
    }
    return 0;  // stub
}

否则，这是有趣的部分，我们必须进行递归调用，找到n−1的阶乘，然后乘以n：

public static int factorial(int n) {
    if (n == 0) {
        return 1;
    }
    int recurse = factorial(n - 1);
    int result = n * recurse;
    return result;
}

为了说明发生了什么，我们将使用临时变量recurse和result。在每个方法调用中，recurse存储n−1的阶乘，result存储n的阶乘。

如果我们使用值3调用阶乘：

由于3不是0，我们跳过第一个分支，计算n−1的阶乘。。。

	因为2不是0，我们跳过第一个分支，计算n−1的阶乘。。。

		由于1不是0，我们跳过第一个分支，计算n−1的阶乘。。。

			因为0是0，所以我们获取第一个分支并立即返回值1。

		返回值（1）乘以n，即1，然后返回结果。

	返回值（1）乘以n，即2，然后返回结果。

返回值（2）乘以n，即3，结果6返回到调用的factorial（3）。

如下显示了这个方法调用序列的堆栈图。返回值显示为向上传递堆栈。请注意，recurse和result在最后一帧中不存在，因为当n==0时，声明它们的代码不会执行。

Java递归方法Recursive详解

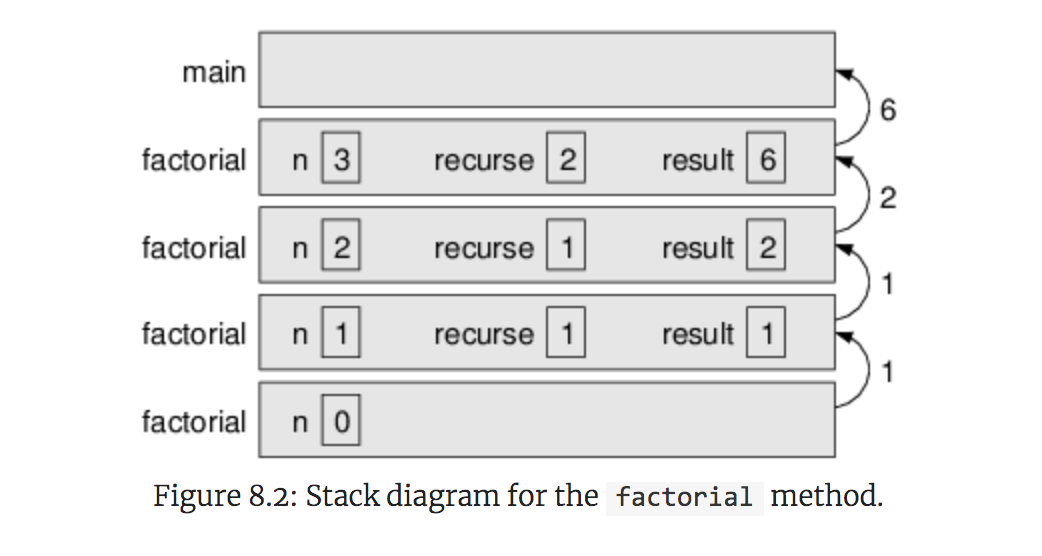
信仰的飞跃

遵循执行流程是读取程序的一种方式，但它很快就会变得势不可挡。理解递归的另一种方法是信心的飞跃：当您进入方法调用时，而不是遵循执行流程，而是假定方法正常工作并返回适当的值。

事实上，当您在Java库中使用方法时，您已经在实践这种信念的飞跃。当你调用数学.cos或者System.out.println，您不会考虑这些方法的实现。你只是假设他们工作正常。

其他方法也是如此。例如，考虑确定整数是否只有一位的方法：

public static boolean isSingleDigit(int x) {
    return x > -10 && x < 10;
}

一旦您通过检查和测试代码来说服自己这个方法是正确的，那么您就可以使用这个方法，而不必再查看实现了。

递归方法也不例外。在进行递归调用时，不要考虑执行流程。生成递归调用，而不是假定所需的结果。

例如，“假设我可以找到n−1的阶乘，我可以计算n的阶乘吗？“是的，你可以用n乘以。下面是一个factorial的实现，去掉了临时变量：

public static int factorial(int n) {
    if (n == 0) {
        return 1;
    }
    return n * factorial(n - 1);
}

请注意，此版本与原始数学定义有多相似：

0！=1

n！=n·（n−1）！

当然，当您还没有写完这个方法时，假设它能正确工作是很奇怪的。但这就是为什么它被称为信仰的飞跃！

另一个常见的递归定义的数学函数是Fibonacci序列，其定义如下：

fibonacci(1) = 1 
fibonacci(2) = 1 
fibonacci(n) = fibonacci(n−1) + fibonacci(n−2)

注意，每个Fibonacci数都是前面两个Fibonacci数的和。这个函数翻译成Java，如下所示：

public static int fibonacci(int n) {
    if (n == 1 || n == 2) {
        return 1;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

如果你试图遵循这里的执行流程，即使是很小的n值，你的头也会爆炸。但是，如果我们相信这两个递归调用是正确的，那么从定义来看，我们的实现是正确的。

递归计数

在倒计时示例的代码有三个部分：

检查基本情况
显示某些内容
进行递归调用

如果您反转步骤2和3，在显示之前进行递归调用，您认为会发生什么情况？

public static void countup(int n) {
    if (n == 0) {
        System.out.println("Blastoff!");
    } else {
        countup(n - 1);
        System.out.println(n);
    }
}

堆栈图和以前一样，方法仍然被调用n次。但是现在System.out.println在每个递归调用返回之前发生。因此，它是递增而不是递减：